Option Calculator
Table of Contents
1. Introduction
1.1 Purpose
This document provides an overview of the SILEXX OEMS Option Calculator Module. It is perfect for pricing FLEX options- adjust pricing model, exercise style, date and more. Provides implied volatility and Greeks.
2. Option Calculator Basics
2.1 Launching a Option Calculator
A Option calculator can be launched by the following these steps:
- Go to Modules Menu
- Navigate to "Option Calculator"
- Right click on this module menu option.
2.2 Navigating the Option Calculator
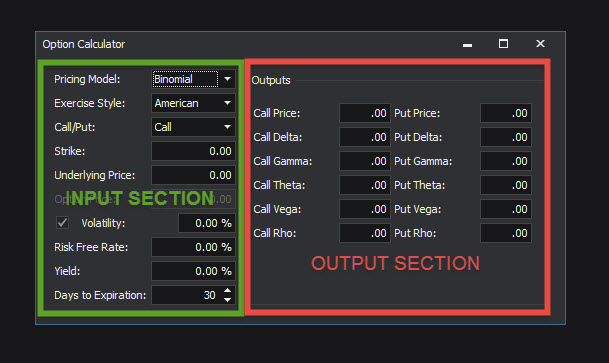
The Option Calculator is broken up into two sections adjacent of each other:
- Input section, allows the user to input customer parameters into the calculator that will drive the output.
- Output section, this area of the option calculator displays various outputs drive by the inputs you have entered example being pricing and option Greeks.
3. Option Calculator In Depth Look
3.1 Option Calculator Input:
- Pricing Model- within the Pricing model input side of the option calculator you as that user have the ability to choose between two models:
- Binomial: The binomial model takes a risk-neutral approach to valuation. It assumes that underlying security prices can only either increase or decrease with time until the option expires worthless.
- Black-Scholes: The Black Scholes model is a model of price variation over time of financial instruments such as stocks that can, among other things, be used to determine the price of a European call option. The model assumes that the price of heavily traded assets follows a geometric Brownian motion with constant drift and volatility. When applied to a stock option, the model incorporates the constant price variation of the stock, the time value of money, the option's strike price and the time to the option's expiry.
- The Black Scholes model uses these necessary inputs to form its calculations:
- The underlying Stock Price
- The option's Strike Price
- Time to the option's expiry
- Volatility of the stock
- Time value of money (or risk free interest rate)
3.2 Option Calculator Output:
A. Output Call Side:
| Field | Description |
|---|---|
| Call Price | Price of the call option |
| Call Delta | Measures an options sensitivity to a change in the price of the underlying. |
| Call Gamma | Gamma measures the rate of change of Delta. Delta tells us how much an option price will change given a one-point move of the underlying. But since Delta is not fixed and will increase or decrease at different rates, it needs its own measure, which is Gamma. |
| Call Theta | Time value decay as a risk variable, it is measured in the form of the (non-constant) rate of its decay, known as Theta. Theta values are always negative for options because options are always losing time value with each tick of the clock until expiration is reached. |
| Call Vega | Measures the risk of gain or loss resulting in changes in volatility. |
| Call Rho | Rho is the rate at which the price of a derivative changes relative to a change in the risk-free rate of interest. Rho measures the sensitivity of an option or options portfolio to a change in interest rate. |
B. Output Put Side:
| Field | Description |
|---|---|
| Put Price | Price of the Put option |
| Put Delta | Measures an options sensitivity to a change in the price of the underlying. |
| Put Gamma | Gamma measures the rate of change of Delta. Delta tells us how much an option price will change given a one-point move of the underlying. But since Delta is not fixed and will increase or decrease at different rates, it needs its own measure, which is Gamma. |
| Put Theta | Time value decay as a risk variable, it is measured in the form of the (non-constant) rate of its decay, known as Theta. Theta values are always negative for options because options are always losing time value with each tick of the clock until expiration is reached. |
| Put Vega | Measures the risk of gain or loss resulting in changes in volatility. |
| Put Rho | Rho is the rate at which the price of a derivative changes relative to a change in the risk-free rate of interest. Rho measures the sensitivity of an option or options portfolio to a change in interest rate. |

To Top